[알린이의 코테 입문 #005 - 008] 사칙연산, 조건문, 배열
Category: Programmers
태그: Programmers
📍 사칙 연산
🔎 문제 1. 두 수의 나눗셈
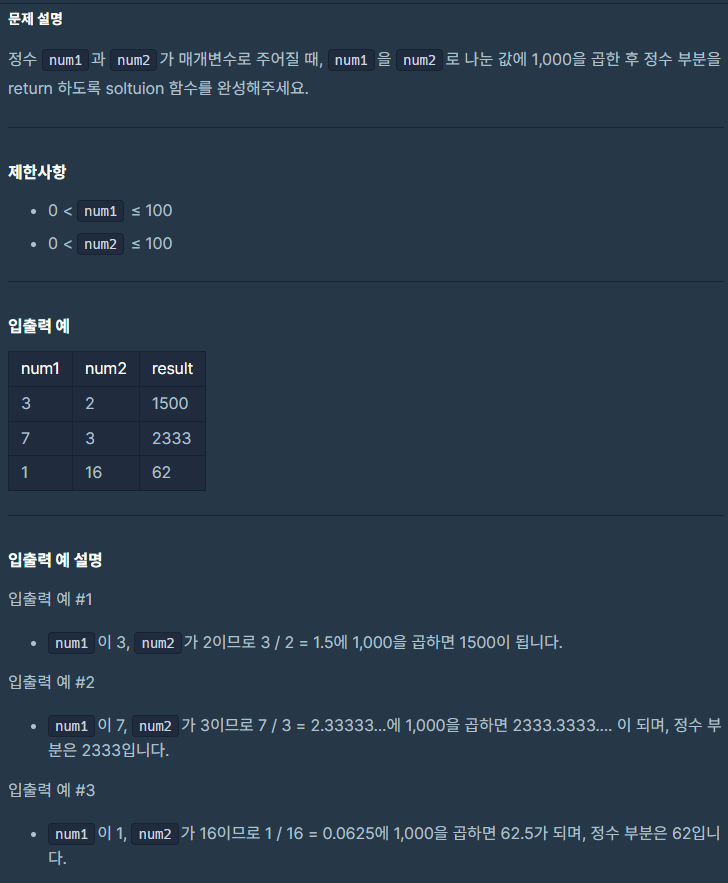
🤔 나의 풀이
using System;
public class Solution {
public int solution(int num1, int num2) {
var result = (float)num1 / num2 * 1000;
return Convert.ToInt32(result);
}
}
처음에 위와 같이 생각했다.
하지만 무언가 문제가 있는지
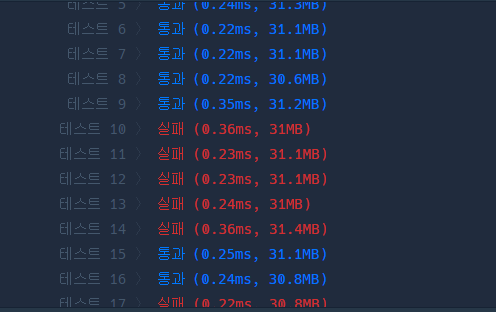
위와 같은 문제가 생겼다. Convert.ToInt32 메서드를 호출하는 과정에서 데이터 손실이 나는게 틀림없다.
따라서 다른 방법으로 접근하는 것은 어떤지 생각을 해봄.
C#에서 소수점 반올림, 올림, 버림 하는 방법에는 Math.Round, Math.Ceiling, Math.Truncate 메서드가 있다.
단 전부 double형 반환 메서드다.
double d = 1.26;
double rd = Math.Round(d); //소수첫짜리 반올림 : 1
double rc = Math.Ceiling(d); //소수첫짜리 올림 : 2
double rt = Math.Truncate(d); //소수첫짜리 버림 : 1
double rd1 = Math.Round(d, 1); //소수둘째자리 반올림 : 1.3, (참고)Math.Round(1.25, 1) => 1.2
double rd2 = Math.Round(d, 2); //소수둘째자리 반올림 : 1.26
double rd3 = Math.Round(d, 3); //소수세째자리 반올림 : 1.26
나는 여기서 Truncate를 사용했고, 아래와 같은 코드를 작성했다.
using System;
public class Solution {
public int solution(int num1, int num2) {
var result = (double)num1 / num2 * 1000;
return (int)Math.Truncate(result);
}
}
아무런 문제없이 통과 되었다.
물론 한줄로 줄일 수도 있지만, 내가 주관적인 의견으로는 굳이 한줄이라도 줄이겠다고 모든 연산식을 한줄에 때려박는 것은 오히려 가독성에 치명적인 결함을 줄 수 있다고 생각한다.
그게 무엇이든지 적당한게 좋다고 생각한다.
🔎 문제 2. 숫자 비교하기
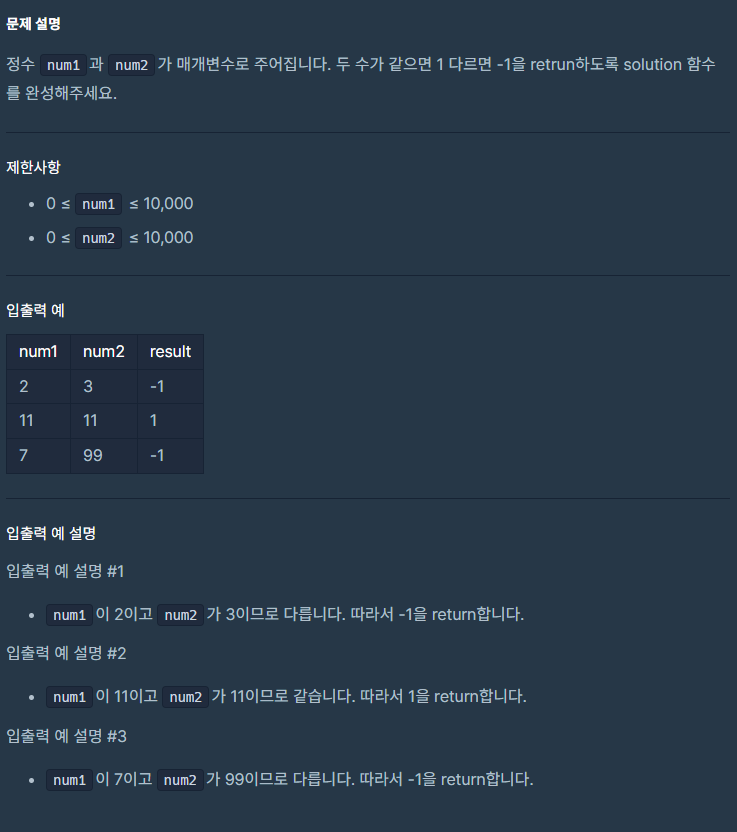
🤔 나의 풀이
using System;
public class Solution {
public int solution(int num1, int num2) {
return num1 != num2 ? -1 : 1;
}
}
삼항 연산자를 써봤다.
🔎 문제 3. 분수의 덧셈
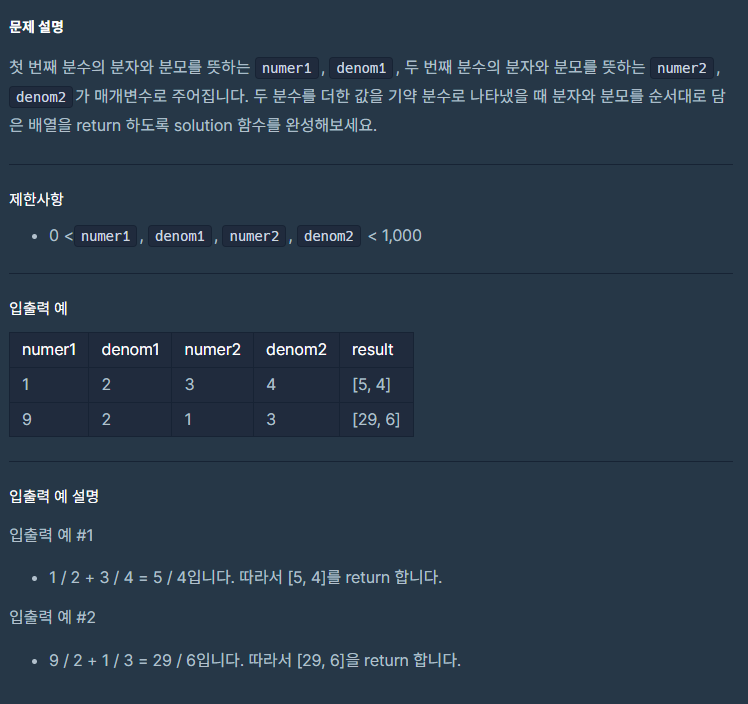
🤔 나의 풀이
먼저 어떻게 풀어야 할지는 어느정도 감이 왔지만, 두 정수의 최대 공약수를 구하는 법은 몰랐다.
그래서 검색을 해봤는데, 유클리드 호제법이라는 알고리즘이 나왔다.
💡 유클리드 호제법
C# 에서 “유클리드 호제법”은 최대 공약수(Greatest Common Divisor, GCD)를 구하는 알고리즘이다.
이 알고리즘은 두 정수 a, b에 대해 GCD(a,b)를 구할 때 a와 b가 주어지면 a와 b의 차를 계산하여 다시 a,b와 a%b로 바꿔서 반복하여 계산한다. 이 과정을 a%b가 0이 될 때까지 반복하여 구한다.
C# 샘플 코드
int GCD(int a, int b)
{
while (b != 0) {
int remainder = a % b;
a = b;
b = remainder;
}
return a;
}
나머지 연산자는 오른쪽의 값으로 왼쪽 값을 나눈 후 남은 나머지를 구한다.
a와 b가 각 10과 8로 주어졌다고 가정하면 b가 0이 아닐 경우, 즉 8이 0이 될 때까지 while문을 계속 해서 반복하게 된다.
본문을 들여다보면 remainder에 10 % 8 의 연산 값을 할당 한다.
따라서 int remainder = 2; 가 되고 a에 b를 할당한다.
a = 8; 그리고 b에 remainder 즉 2를 할당한다.
현재 a = 8, b = 2 이므로 while의 조건식 2 != 0에 true가 되므로 본문을 반복한다.
int remainder = 8 % 2 나머지가 없으므로 0 이나오고 즉 a = 2, b = 0 이 되고,
while의 조건식 0 != 0 이 false가 되므로 while문에서 빠져나와 a값 즉 2를 리턴 한다.
결론적으로 최대공약수는 2가 된다.
While문을 써서 돌리는 건, 이제 이해가 됐는데 뭔가 너무 길다.
좀 더 찾아봤는데, While문을 재귀함수로 작성한 사람도 있었다.
이거 좀 괜찮은데?
바로 가져와서 분석해봤다. 아래는 재귀함수를 사용한 유클리드 호제법이다.
public int gcd(int n, int m)
{
if (m == 0) return n;
else return gcd(m, n % m);
}
우리가 얻어야 할 값은 if(m == 0) return n 이 부분이다.
그렇기 때문에 사실상 gcd(m, n % m) 이 부분을 재귀로 호출해도 언겐가 m은 0이 될테고 return n 으로 빠져나오게 된다.
if - else 문이니까 삼항 연산자로 바꿔주면 아주 깔끔하겠지?
public int gcd(int n, int m)
{
return m != 0 ? gcd(m, n % m) : n;
}
혹시나해서 적어 두는데 n와 m의 순서는 어떤 수를 기준으로 하냐의 차이이지, 꼭 순서를 똑같이 할 필요는 없다.
public static int reversegcd(int n, int m)
{
return n != 0 ? reversegcd(m % n, n) : m;
}

까알끔하다.
추가적으로 이 알고리즘은 매우 효율적이고, 일반적으로 빠른 결과를 제공한다고 한다.
🚀 제출한 코드
using System;
public class Solution {
public int[] solution(int numer1, int denom1, int numer2, int denom2) {
var _numer = numer1 * denom2 + numer2 * denom1;
var _denom = denom1 * denom2;
var _gcd = gcd(_numer, _denom);
return new[] { _numer / _gcd, _denom / _gcd };
}
public int gcd(int n, int m)
{
return m == 0 ? n : gcd(m, n % m);
}
}
🌈 번외 - 최소공배수
최소 공배수의 공식은 두수의 곱 / 최대 공약수이므로
a * b / GCD(a ,b);
이렇게 구할 수 있다.
위의 코드를 눈에 익게 만들자.
두 수의 최소/최대 공약수, 공배수의 값을 구하는 것은 항상 매번 언급되는 기본적인 알고리즘이다.
외우라는 것은 아니지만 여러가지 예제를 만들어서 복습하는 것도 좋을 것 같다.
따로 정리를 해둬야 겠다.
🔎 문제 4. 배열 두 배 만들기

🤔 나의 풀이
using System;
public class Solution {
public int[] solution(int[] numbers) {
for(var i = 0; i < numbers.Length; i ++)
numbers[i] *= 2;
return numbers;
}
}
🤣 한마디
알지못하는 알고리즘이 나왔었다.
예제를 많이 만들어서 복습하도록!
이 게시물에는 지극히 주관적인 생각이 포함되어 있습니다.
오류나 틀린 부분, 또는 수정해야 할 부분이 있다면 언제든지 댓글 혹은 메일로 지적 부탁드립니다.

Comment