Victor Ji 🐯

Victor Ji 🐯

호랑이에 진심인 개발자

Big O 표기법이 뭔지 도저히 몰라서 팝핀 댄스를 추고 싶을 때 보려고 쓴 글

Data:     Updated:

Category:

태그:

💡 이걸 왜 알아야 하죠?

물론 몰라도 상관없다.

하지만 이것을 몰라도 상관없다는 얘기는 시간복잡도를 고려하지 않아도 될 정도의 간단한 일을 하고 싶다는 것을 방증하는 것과 같다.

이 개념을 모르면 다른 플머들과 협업할 때 혼자 이해를 못하는 상황이 오고, 시간 복잡도 자체를 모른다면 성능의 최적화는 이번생에는 먼 얘기가 된다.


💁‍♂️ Big-O 표기법이 뭔가요?

빅 OOOOOOOOOOOOOOOOO 알고리즘의 성능을 수학적으로 표기해주는 표기법이다. 이 표기법으로 알고리즘의 시간, 공간 복잡도를 표현할 수 있음.

Big O는 알고리즘의 실제 러닝 타임이 아닌 데이터나 사용자의 증가율에 따른 알고리즘의 성능을 예측하는 것이 목표이기 때문에, 상수와 같은 숫자는 모두 무시한다.

선형 검색(Linear search)을 예를 들어 설명할 것이다.
선형 검색은 하나씩 하나씩 검색을 한다.

그래서 데이터가 10개라면 한개씩 검색을 하기 때문에 시간복잡도는 상수로 10 이고,
데이터가 20개 라면? 20개 전부를 검색해야 하니 시간복잡도는 상수로 20 이 되는 것이다.

따라서 데이터의 개수가 N 이라면 선형 검색 알고리즘은 N 만큼의 시간이 걸리는 것이다. 이것을 빅O 표기법으로 하면 아래와 같은 O(n)으로 표기 된다.

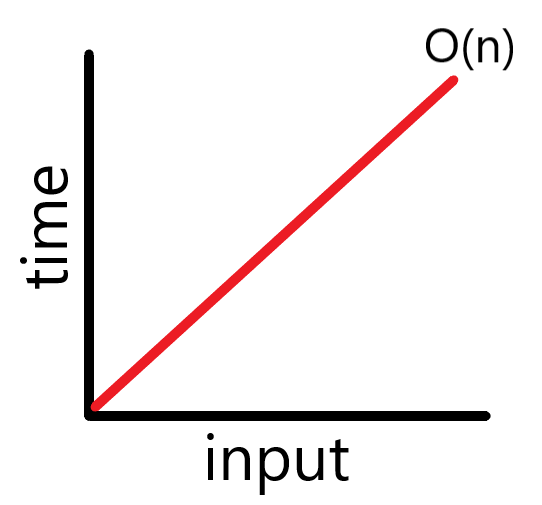
img01

데이터의 개수가 N개면 N 만큼의 시간이 필요하다. = O(N)


💁‍♂️ 그래서 배우면 좋은 점이 뭐죠?

Big O를 이해하면, 알고리즘 분석을 빠르게 할 수 있고 언제 무엇을 쓸지 빠르게 파악이 가능하다.

그리고 시간복잡도를 표기함으로써 내가 만든 코드의 평가를 내릴 수 있다. 왜냐하면 미래에 어떻게 작동할 지 알 수 있기 때문이다.


💁 자 그러면 이제 Big O 들어간다 입을 O하고 벌려

🔖 O(1) Algorithms (constant time)

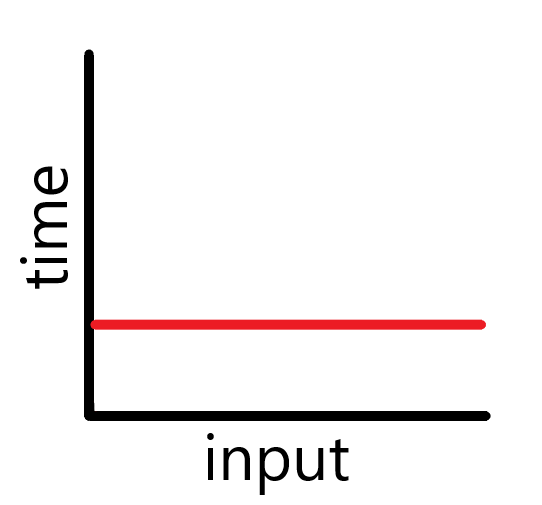
데이터의 증가함에 따라 성능에 변함이 없음.

상수 시간이라고도 하는데, 어떤 문제를 풀이할 때 필요한 수학적 연산 시간이 주어진 입력 자료에 관계 없이 일정할 때의 연산 시간을 의미한다.

🔔 상수 시간 위키 설명

public void Method(int[] n)
{
    Console.WriteLine(n[0]);
}

위와 같은 메서드가 있다고 가정하자 매개변수로 int 배열을 받아와서 배열의 첫번째 요소를 출력하는 것이다.

이 메서드는 배열의 크기가 10이 돼도 100이 돼도 단 한번만 실행을 한다. 따라서 배열의 크기와 관계 없이 동일한 수의 스텝만 실행한다.

이 메서드의 시간복잡도는 constant time(상수 시간) 이라고 할 수 있다.

img02

public void Method(int[] n)
{
    Console.WriteLine(n[0]);
    Console.WriteLine(n[0]);
}

방금 전의 코드에서 변경된 건 단지 출력을 두번하는 것 뿐이다.
(설명하기 쉽게 방금 전의 코드를 A code, 현재의 코드를 A’ code 라고 지칭하겠다.)

그렇다면 방금 전의 코드 A code 에서 시간 복잡도가 O(1) 이었으니 A’ code 의 시간 복잡도는 O(2)인걸까?

답은 아니다.

여전히 동일하게 O(1) 라고 표현하는데, 그 이유는 Big O 표기법은 메서드의 디테일에는 관심이 없기 때문이다.

Big O 는 러프하게 이 메서드가 데이터의 크기에 따라 어떻게 동작하는지에 대한 큰 원리에만 관심이 있다.

따라서 Big O를 이해하려면 이 표기법은 상수 (constant)에 전혀 신경을 쓰지 않는 다는 것을 꼭 기억해야 한다.

결론적으로 위의 메서드에서 배열의 크기가 10, 100, 1000, 1000000000이 된다고 해도 시간 복잡도는 여전히 O(1)로 표기되는 것이다.

🔖 O(n) Algorithms (linear time)

데이터에 증가함에 따라 비례해서 처리시간도 늘어남.

public void Method(int[] n)
{
    foreach (var i in arr)
        Console.WriteLine(i);
}

위의 코드는 배열의 모든 요소를 출력하는 코드이다. 만약 배열의 크기가 10개면 10번, 100개면 100번 출력하게 될 것이다.

이 작동 방식은 선형 검색 알고리즘과 동일하다. 배열의 크기가 N일 경우 N번의 스텝을 걸쳐야 하기 때문이다.

이건 Big O 표기법으로 O(n)으로 표기한다.

그렇다면 이것은 어떨까?

public void Method(int[] n)
{
    foreach (var i in n)
        Console.WriteLine(n);
    
    foreach (var i in n)
        Console.WriteLine(n);
}

이 코드의 시간 복잡도는 각 N마다 2번 작업을 하니 O(2N) 으로 표기하는 걸까?

답은 아니다. 2는 상수이기 때문에 날려버리고 O(N)으로 표현하게 된다.

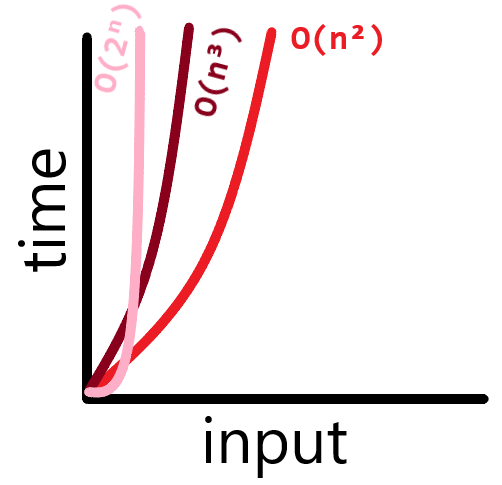
🔖 O(n²) Algorithms (quadratic time)

데이터가 커지면 커질 수록 처리시간이 기하급수로 올라감 to the moon.

public void Method(int[] n)
{
    foreach (var i in n)
        foreach (var j in n)
            Console.WriteLine($"{i+j}");
}

이 코드는 배열의 각 아이템에 대하여 루프를 반복해서 실행한다. 따라서 시간복잡도는 배열의 크기의 n² 인 것이고, 이 말은 배열의 크기가 10이라면 작업이 완료 되는데 10의 제곱인 100번의 스텝이 필요한 것이다.

이것은 Big O 표기법으로 O(n²) 이다.

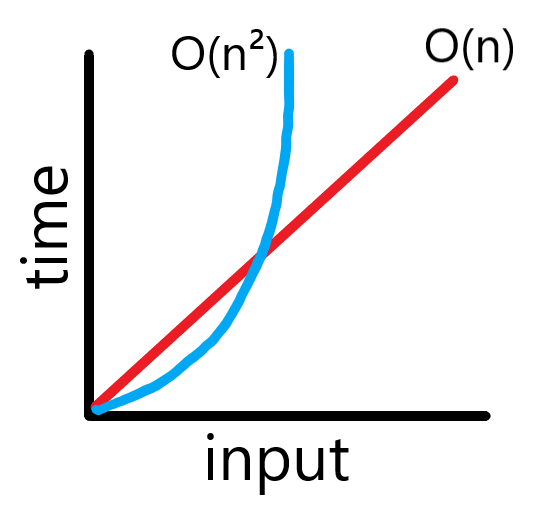
img03

따라서 위의 코드 보다는 선형 검색 알고리즘 시간 복잡도가 더 효율적인 것을 알 수 있다.

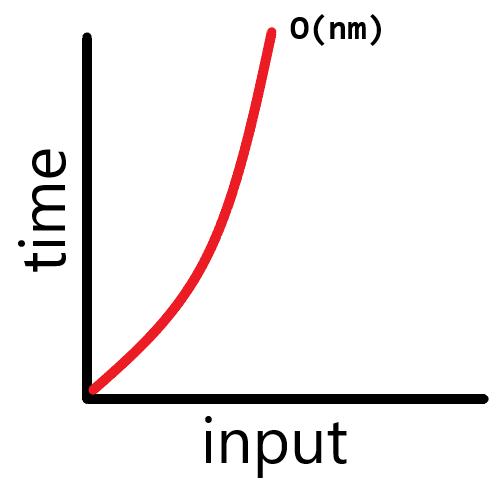
🔖 O(nm) Algorithms (quadratic time)

코드와 그래프의 모양이 O(n²) Algorithms와 같아서 유의해서 표기 해야함. n 배열을 2번 돌리는게 아닌 m 배열을 n 배열 만큼 돌리는 것 이기 때문이 이것은 엄연히 다른 알고리즘이다. (n이 m보다 작을수도 클수도 있기 때문이다.)

public void Method(int[] n, int[] m)
  {
      foreach (var i in n)
          foreach (var j in m)
              Console.WriteLine($"{i+j}");
  }

img03-1

🔖 O(n³) Algorithms (polynomial / cubic time)

[이해를 쉽게하기 위한 이미지]

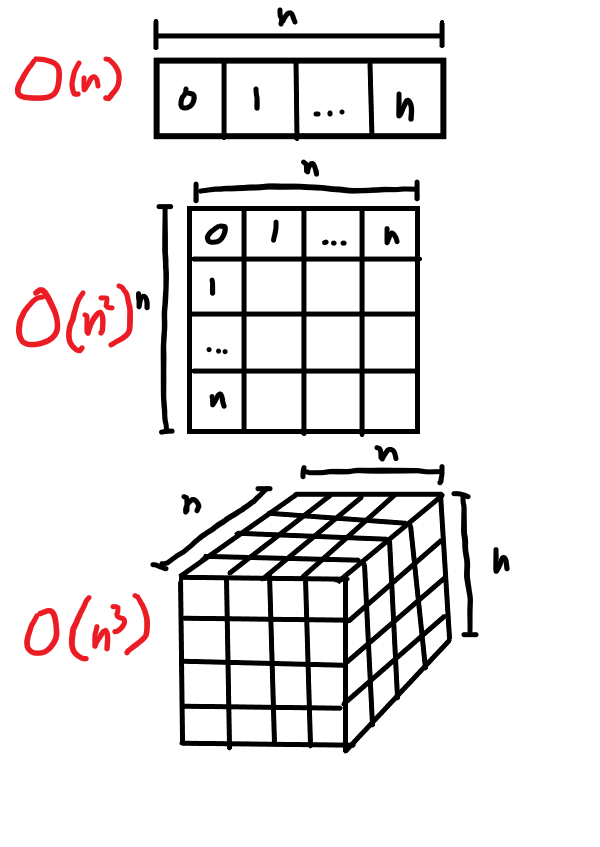
img03-2

public static void Method(int[] n)
    {
        foreach (var i in n)
            foreach (var j in n)
                foreach (var k in n)    
                    Console.WriteLine($"{i+j+k}");
    }

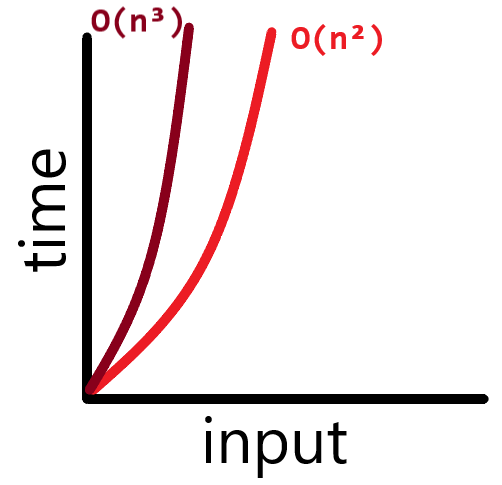
O(n³) Algorithms는 그래프에서 O(n²) Algorithms와 비슷한 양상을 보이지만 처리시간의 증가가 더 급격하게 일어난다.

img03-3

🔖 O(2ⁿ) Algorithms (exponential time)

Fibonacci 수열 - 1 부터 시작해서 한면을 기준으로 정사각형을 만드는 것

Fibonacci 수열도 나중에 심도있게 다루겠음.

이해를 쉽게하기 위한 이미지

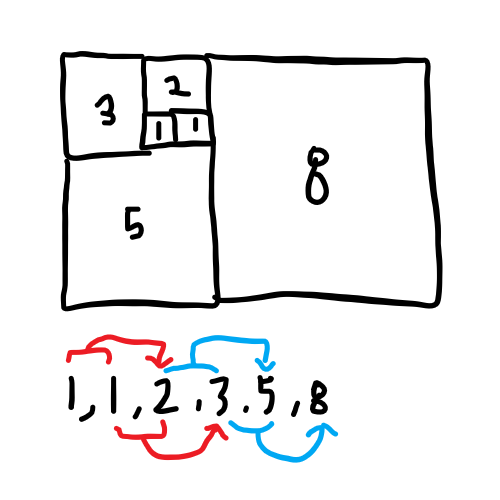
img03-4

Fibonacci 수열을 재귀함수를 이용해서 코드를 작성하면 아래와 같이 된다.

public int Fibonacci(int n, int[] r)
{
    if (n <= 0)
        return 0;
    if (n == 1)
        return r[n] = 1;

    return r[n] = Fibonacci(n - 1, r) + Fibonacci(n - 2, r);
}

작동 방식을 이미지로 표현하면 아래와 같음.

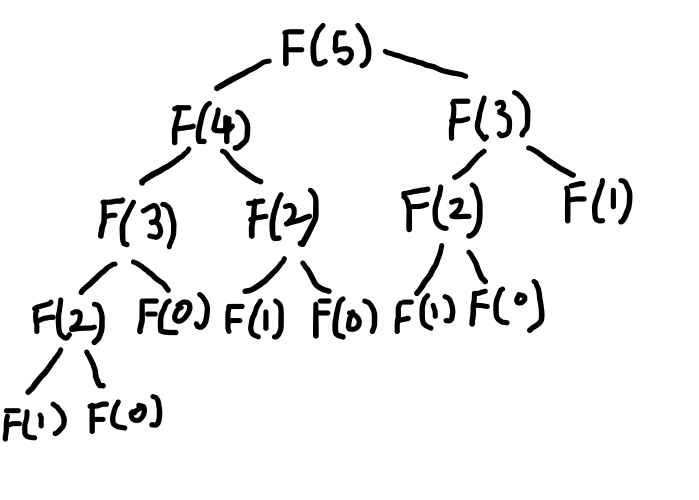
img03-5

그래프

img03-6

🔖 O(log n) Algorithms

또 다른 시간 복잡도로는 로그 시간 (Logarithmic time) 이 있다. 이것은 이진 검색 알고리즘을 설명할 때 쓰는 것이다.

10 items -> 20 items
3 steps -> 4 steps

이진 검색은 배열의 크기가 2배가 되어도, 스텝은 단 1 밖에 증가하지 않는다. 왜냐하면 이진 검색에서는 각 프로세스의 스텝을 절반으로 나눠서 진행하기 때문이다.

이것을 Big O로 표현하면, O(log N)이 된다.

이진 검색 알고리즘은 다음번에 심도있게 다룰 것임, 그 후에 코드를 올리겠음.

로그(logarithm)는 지수(exponent)의 정 반대다.

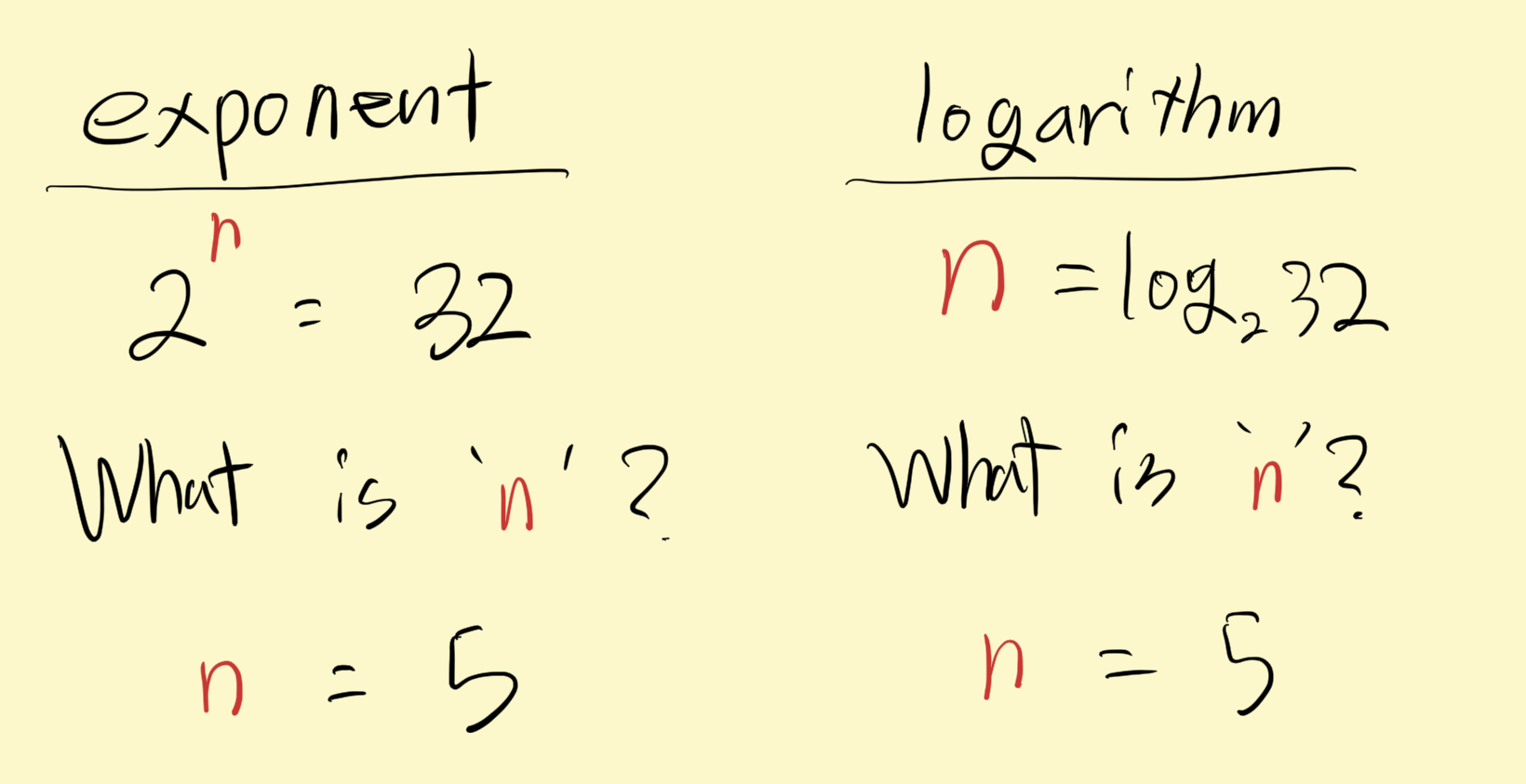
img04

이어서 이진 검색에 대해서 계속 말하자면, 배열의 크기를 일단 반으로 나누고 시작한다. 그리고 매 스텝마다 계속 반으로 나눈다. 따라서 배열의 크기가 2배로 커져도, 검색을 하기 위한 스텝은 1 만 증가하게 된다.

왜냐면 한번만 더 나누면 되는 것이기 때문이다.

결론적으로 이진 검색의 Big O 식 시간 복잡도는 O(log n) 인데, 그 이유는 Big O의 특성상 Base는 사라지기 때문이다.

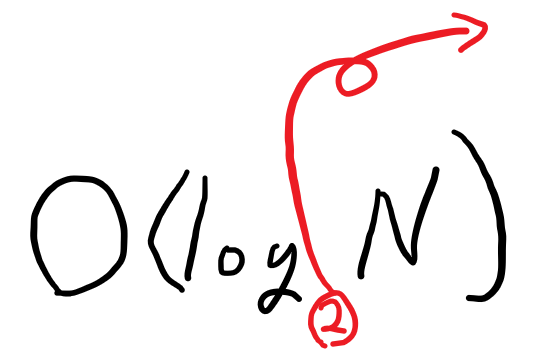
img05

O(log n)의 그래프의 모습은 아래와 같다.

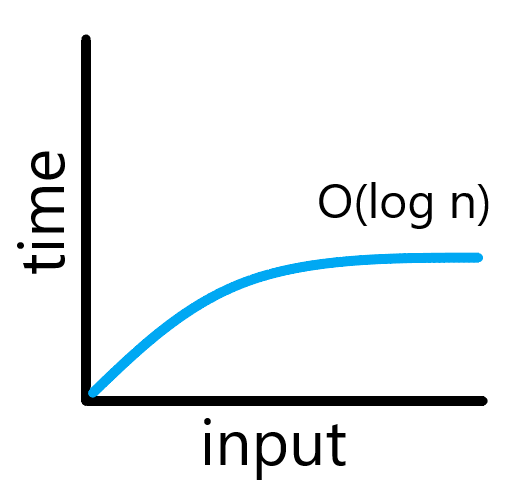
img06

그리고 이것은 선형 검색 알고리즘보다는 빠르다. 하지만 이진 검색에는 조건이 존재하는데, 그 조건은 정렬되지 않은 배열엔 사용할 수 없다는 것이다.

😩 시간 복잡도를 줄이는 방법?

1. 시간 복잡도에서 반복문이 시간 소모에 가장 큰 영향을 미치기 때문에, 반복문의 숫자를 줄이는 것이다.  
2. 자료구조를 적절하게 이용한다.
3. 알고리즘을 적절하게 이용한다.

🧨 자료구조 시간 복잡도 표

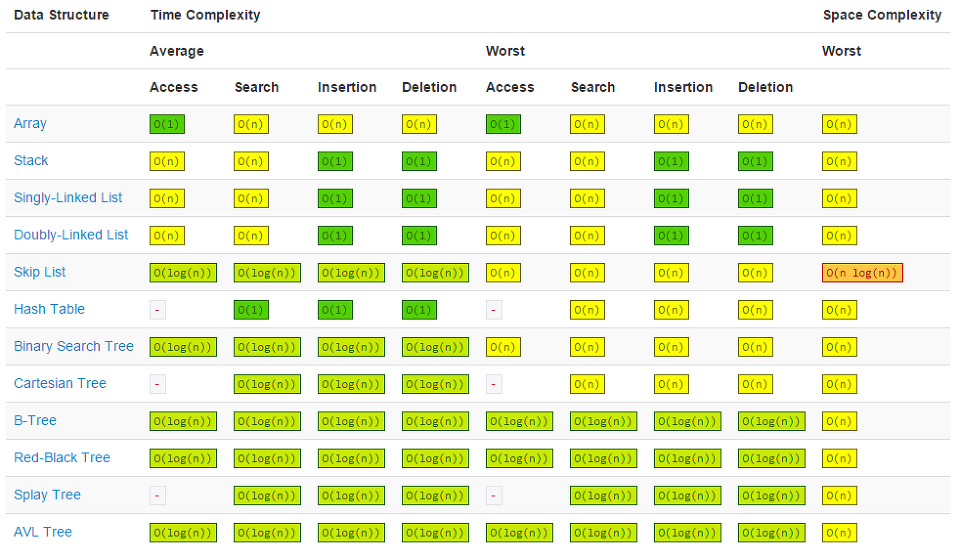
img07

🧨 알고리즘 시간 복잡도 표

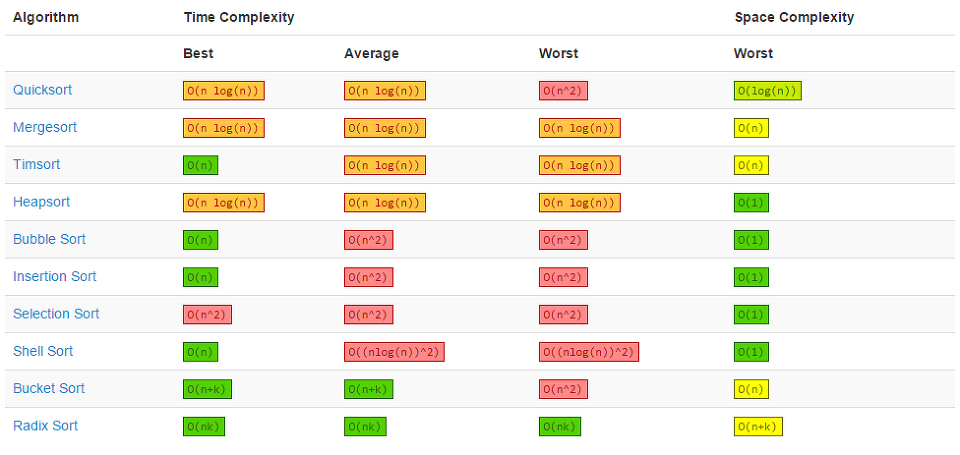
img08


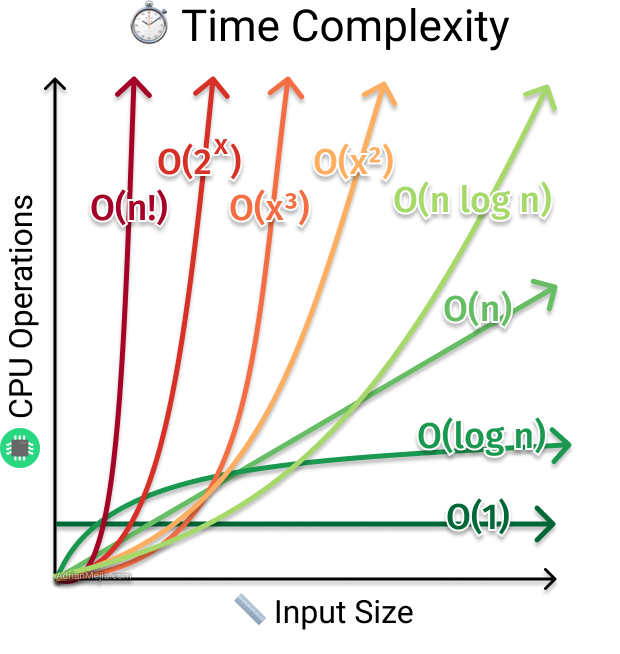
🎯 총정리 그래프

마지막으로 이 글을 머리 속에 박아버리고 그래프를 확인해보자.

✨✨Big O는 대충 살아서 상수 같은건 버려.✨✨


img09

🔎 참고한 내용

🔔 노마드 코더 Nomad Coders 님의 Big O 설명 10분 컷 영상
🔔 코딩팩토리님의 블로그


끝

이 게시물에는 지극히 주관적인 생각이 포함되어 있습니다. 
오류나 틀린 부분, 또는 수정해야 할 부분이 있다면 언제든지 댓글 혹은 메일로 지적 부탁드립니다.

Top

Dev Dictionary Go to see other posts in the category

Comment

🍳 Recent Posts Top 10 🍳